DIY: Primality Testing with Miller-Rabin

We’ve all had to include a little isprime() function in our code, right? (well, most people reading my blog probably have). In this article i provide an implementation of a primality test (in C) that is quite a bit faster for larger values, and is still easily embeddable and usable within existing applications

References:

Naive Implementation

Most programmers, when asked to check whether a number is prime, would probably write some code like the following (myself included):

1
// check whether 'n' is prime, using a naive method
2
bool
3
isprime_naive(size_t n) {
4
    // take care of 0,1
5
    if (n < 2) return false;
6
    // get rid of even numbers, except 2
7
    if (n % 2 == 0) return n == 2;
8

9
    // do trial division, checking only the odd numbers <= sqrt(n)
10
    size_t i;
11
    for (i = 3; i * i <= n; i += 2) {
12
        // divisible, so not prime
13
        if (n % i == 0) return false;
14
    }
15

16
    // no factors, so must be prime
17
    return true;
18
}

While there’s nothing wrong with this code, and it arguably is the best solution if you only use it a couple of times, there are more efficient deterministic tests for larger numbers. For example, we’ll look at using the Miller-Rabin primality test, modified to be deterministic for a suitable range of ‘n’

Miller-Rabin implementation

I’m just going to include the full implementation here, so you can copy and paste, and read the comments to understand how it works:

1
/* Miller-Rabin 'isprime()' implementation
2
 *
3
 *
4
 * NOTE: https://en.wikipedia.org/wiki/Miller%E2%80%93Rabin_primality_test
5
 * @name: Cade Brown <cade@cade.site>
6
 */
7

8
// (internal) compute a**b (mod m)
9
static size_t
10
my_modpow(size_t a, size_t b, size_t m) {
11

12
    // a**2**i (mod m)
13
    usize a2i = a;
14

15
    // the result product
16
    usize res = 1;
17

18
    // basically, iterate over the bits of 'b', and treat it
19
    //   as a bitset
20
    while (b) {
21
        if (b & 1) {
22
            // this power should be included, since its in the bitset
23
            res = (res * a2i) % m;
24
        }
25

26
        // compute, and apply modulo to avoid overflow:
27
        // a**2**(i+1) == (a**2**i)**2
28
        a2i = (a2i * a2i) % m;
29

30
        // now, shift the bitset
31
        b >>= 1;
32
    }
33

34
    return res;
35
}
36

37
// (internal) perform a witness check in Miller-Rabin, returns whether it is probably prime
38
//   a: the witness being tested
39
//   n: the number being checked for primality, n := 2**r * d + 1 (i.e. within the 2-adic number system)
40
//   r: see 'n'
41
//   d: see 'n', must be ODD
42
static bool
43
my_witness(size_t a, size_t n, size_t r, size_t d) {
44
    // compute a ** d (mod n)
45
    size_t x = my_modpow(a, d, n);
46

47
    // special case that it's probably true for this witness
48
    if (x == 1 || x == n - 1) {
49
        return true;
50
    }
51

52
    // repeat (r-1) times
53
    size_t ct;
54
    for (ct = 0; ct < r - 1; ct++) {
55
        x = (x * x) % n;
56
        if (x == n - 1) {
57
            // probably true as well
58
            return true;
59
        }
60
    }
61

62
    return false;
63
}
64

65

66
// tell whether 'n' is prime
67
bool
68
isprime(size_t n) {
69
    if (n < 2) return false;
70
    if (n % 2 == 0) return n == 2;
71

72
    // compute: n := 2 ** r * d + 1
73
    // (i.e. decompose into 2-adic number)
74
    size_t d = n - 1;
75
    size_t r = 0;
76
    while (d % 2 == 0) {
77
        r++;
78
        d >>= 1;
79
    }
80

81
    // utility macro for a single witness
82
    #define WIT(_a) my_witness((_a), n, r, d)
83

84
    // use proven bounds
85
    /**/ if (n < 2047ULL) return WIT(2);
86
    else if (n < 1373653ULL) return WIT(2) && WIT(3);
87
    else if (n < 9080191ULL) return WIT(31) && WIT(73);
88
    else if (n < 25326001ULL) return WIT(2) && WIT(3) && WIT(5);
89
    else if (n < 3215031751ULL) return WIT(2) && WIT(3) && WIT(5) && WIT(7);
90
    else if (n <= 0xFFFFFFFFULL) return WIT(2) && WIT(7) && WIT(61); // 32 bit values
91
    else {
92
        // this is a catch all, which should work up to
93
        // 18446744073709551616 = 2**64
94
        // so, this is only needed on 32 bit systems
95
        return WIT(2) && WIT(3) && WIT(5) && WIT(7) && WIT(11) && WIT(13) && WIT(17) && WIT(19) && WIT(23) && WIT(29) && WIT(31) && WIT(37);
96
    }
97
}

Here’s how they perform on my machine, calculating whether 10 million random numbers are prime, within different bounds:

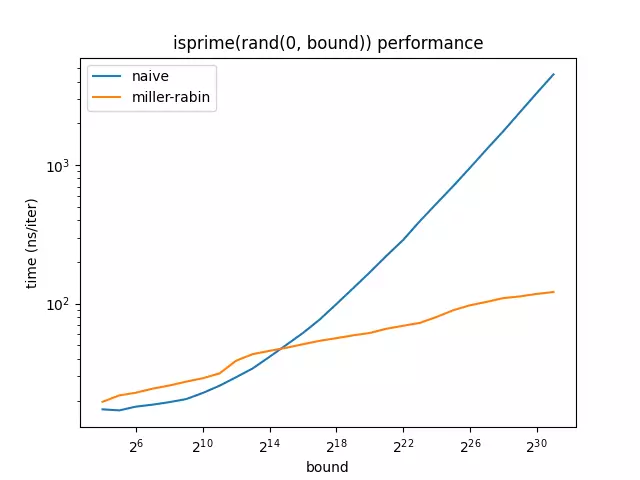
As you can see, both implementations have similar performance (with naive being a little faster), until $2^{14}$ , at which point the trend reverses. The trends become even more pronounced after $2^{32}$ , where the Miller-Rabin implementation essentially always hits the ‘else’ case, and plateaus.

For large values, the Miller-Rabin implementation 30x-50x faster than the naive one! I know this implementation has helped many of my other projects efficiently implement prime checking (check out PGS!)