Dense Linear Algebra Algorithms on AMD GPUs

Number of nonzero digits in representation of n in primorial base.

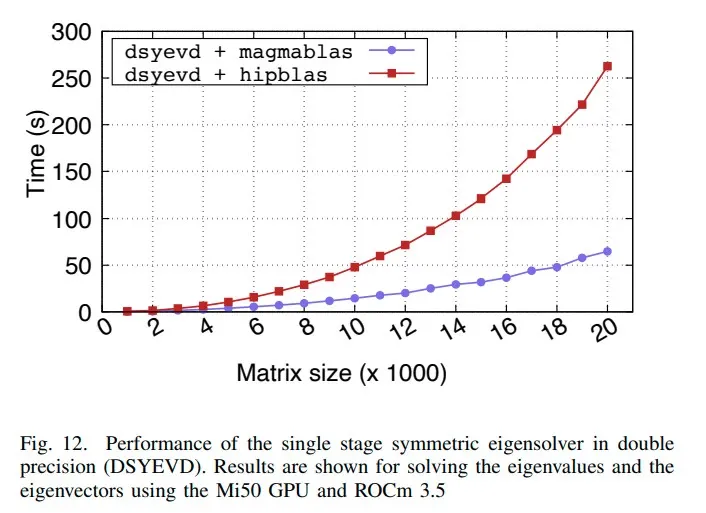
I published my first paper Design, Optimization, and Benchmarking of Dense Linear Algebra Algorithms on AMD GPUs, which was published in IEEE HPEC 2020. This was a major project of mine at ICL that aimed to take the existing MAGMA library that ran on NVIDIA GPUs, and port it to AMD GPUs. Specifically, it needed to work on the Frontier supercomputer at ORNL, which has AMD GPUs.

Interestingly, my co-author won the Turing award. He is a legend in the HPC community, and I was very honored to work with him.

TL;DR: we were able to get 73% faster time-to-solution for solvers, and up to 60x faster for BLAS operations.

We tuned various algorithms (matrix multiplication, rank-k updates) that are common building blocks of machine learning, physical simulations, and other applications. There were a number of obstacles to extracting good performance out of the new hardware; specifically the change in warp size (32 -> 64), new compiler (NVIDIA’s nvcc -> AMD’s ROCm/hipcc), and overall higher peak performance of newer hardware. So much of the HPC ecosystem was built around CUDA, and luckily AMD’s HIP was very similar conceptually.

You can access it at these places:

• at ICL’s PDF
• at Semantic Scholar
• at HGPU
• at OS hackathon’s resources